Here’s an interesting thing that I came across when evaluating a mailing for a client that I need to share.
The observation
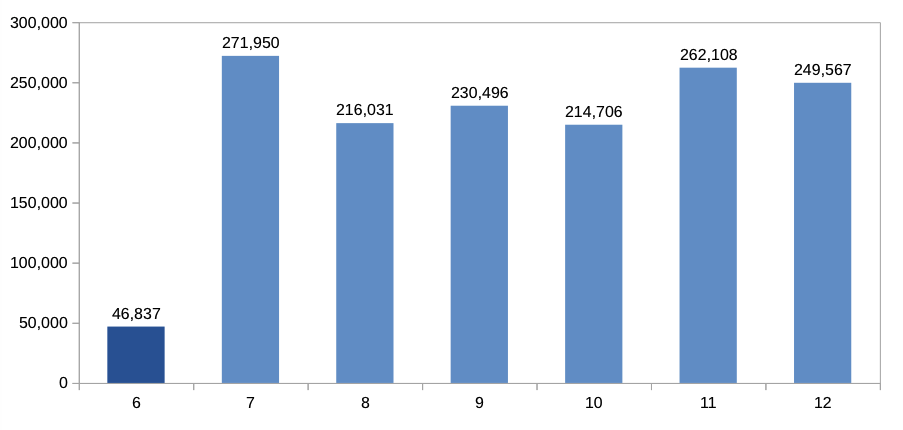
So what we’re looking at here is the revenue for a given group of customers from 06/2014 to 12/2014. (Note that the data presented here is completely fictional recreated in a spreadsheet, but follows patterns similar to the original data. See below for more details.)
This group of customers had been selected due to its inactivity as defined by the revenue in 06/2014 being smaller then a certain threshold (again, the actual selection was a lot more refined that is described in this model).
The mailing was sent out on 01/07/2014 to the group of customers. So we’re looking at a total revenue of $46,837 in 06/2014 and a subsequent jump in revenue to $271,950 in 07/2014.
At first sight, that seems to be great news – the mailing worked, revenue increased drastically, everything fine.
However, when I looked at preceding months, the following pattern emerged:
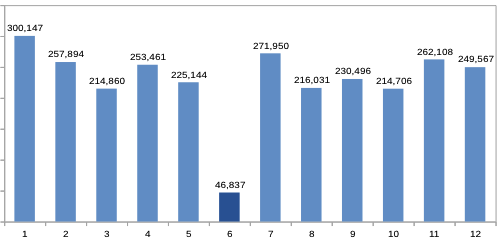
So our group of customers had a high revenue 01/2014 – 05/2014. Then in 06/2014 – the month that was used to determine whether or not a customer was active – the revenue suddenly drops by about 80%, only to be back at the original level the following months.
Now this seems rather odd. In fact, it looks a lot like there’s something wrong with the analysis.
But as it turns out, it’s actually perfectly correct. What we’re observing is due to what I call the selection bias.